Страница 4
1. Прочитайте числа.
В какой из записей цифра 5 обозначает число сотен, в какой — число десятков, в какой — число единиц?
Что обозначает каждая из цифр в записи числа: 555, 333, 888?
Ответ:
В числе 594 цифра 5 стоит в разряде сотен и обозначает 5 сотен.
В числе 451 цифра 5 стоит в разряде десятков и обозначает 5 десятков.
В числе 275 цифра 5 стоит в разряде единиц и обозначает 5 единиц.
В числе 555 цифра 5 стоит в разряде сотен, десятков и единиц и обозначает 5 сотен, 5 десятков и 5 единиц.
В числе 333 цифра 3 стоит в разряде сотен, десятков и единиц и обозначает 3 сотни, 3 десятка и 3 единицы.
В числе 888 цифра 8 стоит в разряде сотен, десятков и единиц и обозначает 8 сотен, 8 десятков и 8 единиц.
Страница 5
2. Что обозначает каждая цифра в записи числа: 67, 290, 666, 400, 101?
Ответ:
В числе 67:
- цифра 6 стоит в разряде десятков и обозначает 6 десятков.
- цифра 7 стоит в разряде единиц и обозначает 7 единиц.
В числе 290:
- цифра 2 стоит в разряде сотен и обозначает 2 сотни.
- цифра 9 стоит в разряде десятков и обозначает 9 десятков.
- цифра 0 стоит в разряде единиц и обозначает 0 единиц.
В числе 666:
- цифра 6 стоит в разряде сотен и обозначает 6 сотен.
- цифра 6 стоит в разряде десятков и обозначает 6 десятков.
- цифра 6 стоит в разряде единиц и обозначает 6 единиц.
В числе 400:
- цифра 4 стоит в разряде сотен и обозначает 4 сотни.
- цифра 0 стоит в разряде десятков и обозначает 0 десятков.
- цифра 0 стоит в разряде единиц и обозначает 0 единиц.
В числе 101:
- цифра 1 стоит в разряде сотен и обозначает 1 сотню.
- цифра 0 стоит в разряде десятков и обозначает 0 десятков.
- цифра 1 стоит в разряде единиц и обозначает 1 единицу.
3. Запишите цифрами число, в котором:
четыре сотни, четыре десятка, восемь единиц;
девять сотен, пять единиц;
девять сотен, пять десятков.
Ответ:
448; 905; 950.
4. Запишите в виде суммы разрядных слагаемых каждое из чисел: 327, 638, 418, 999, 207, 270, 620.
Ответ:
327 = 3 • 100 + 2 • 10 + 7
638 = 6 • 100 + 3 • 10 + 8
418 = 4 • 100 + 1 • 10 + 8
999 = 9 • 100 + 9 • 10 + 9
207 = 2 • 100 + 7
270 = 2 • 100 + 7 • 10
620 = 6 • 100 + 2 • 10
5. Числа представлены в виде суммы разрядных слагаемых. Какие это числа?
6 • 100 + 9 • 10 + 2 1 • 10 + 8
1 • 100 + 3 • 10 7 • 100 + 5
Проверьте себя: найдите ответы среди чисел 705, 130, 18, 692.
Ответ:
6 • 100 + 9 • 10 + 2 = 692
1 • 100 + 3 • 10 = 130
1 • 10 + 8 = 18
7 • 100 + 5 = 705
Страница 6
6. Запишите все возможные трёхзначные числа, используя цифры 8, 0 и 5 так, чтобы в записи каждого числа:
1) цифры не повторялись;
2) цифры повторялись.
Ответ:
1) 508, 580, 805, 850.
2) 500, 505, 508, 550, 555, 558, 580, 585, 588, 800, 805, 808, 850, 855, 858, 880, 885, 888.
7. Приведите примеры двузначных чисел, в которых число единиц в 2 раза меньше числа десятков.
Ответ:
Если десятков 9, то единиц: 9 - 2 = 7. Это число 97.
Если десятков 8, то единиц: 8 - 2 = 6. Это число 86.
Если десятков 7, то единиц: 7 - 2 = 5. Это число 75.
Если десятков 6, то единиц: 6 - 2 = 4. Это число 64.
Если десятков 5, то единиц: 5 - 2 = 3. Это число 53.
Если десятков 4, то единиц: 4 - 2 = 2. Это число 42.
Если десятков 3, то единиц: 3 - 2 = 1. Это число 31.
Если десятков 2, то единиц: 2 - 2 = 0. Это число 20.
8. Проследите, какое число обозначает каждая из семи римских цифр.
Ответ:
I → 1
V → 5
X → 10
L → 50
C → 100
D → 500
M → 1000
9. 1) Проанализируйте записи чисел от 2 до 20 римскими цифрами. Попробуйте сформулировать правила записи чисел.
2) Запишите римскими цифрами числа: 25, 30, 48, 51, 120, 600.
Ответ:
Страница 7
10. В каком году построен замок? Какое время показывают часы?
Ответ:
Замок построен в 1514 году.
Часы показывают 3 ч 23 мин.
11. Вычислите устно.
25 + 6 40 • 6 80 : 2
130 - 20 120 : 30 15 • 4
12 • 4 681 - 600 230 + 70
51 : 17 64 + 36 100 - 75
Ответ:
25 + 6 = 31 40 • 6 = 240 80 : 2 = 40
130 - 20 = 90 120 : 30 = 4 15 • 4 = 60
12 • 4 = 48 681 - 600 = 81 230 + 70 = 300
51 : 17 = 3 64 + 36 = 100 100 - 75 = 25
12. Чем похожи и чем различаются выражения 48 : 6 + 26 • 2 и (48 : 6 + 26) • 2?
Выполните вычисления.
Ответ:
Сходства: в обоих выражениях одинаковые числа и арифметические знаки.
Различие: В первом выражении нет скобок, а во втором - есть, поэтому порядок выполнения арифметических действий отличается.
48 : 6 + 26 • 2 = 8 + 26 • 2 = 8 + 52 = 60
(48 : 6 + 26) • 2 = (8 + 26) • 2 = 34 • 2 = 68
Страница 8
13. Запишите выражения и вычислите их значения.
Из числа 760 вычесть частное чисел 60 и 4.
Произведение чисел 17 и 5 уменьшить на 38.
Частное чисел 52 и 4 увеличить в 5 раз.
Сумму чисел 120 и 60 уменьшить в 90 раз.
Ответ:
760 - 60 : 4 = 760 - 15 = 745
17 • 5 - 38 = 85 - 38 = 47
52 : 4 • 4 = 13 • 5 = 65
(120 + 60) : 90 = 180 : 90 = 2
14. Вычислите.
750 - 560 96 : 8 45 • 9
144 + 38 640 : 20 129 • 5
375 - 29 990 : 30 16 • 24
546 + 128 72 : 6 46 • 15
105 • 15 840 : 210 432 : 108
Ответ:
15. Вычислите значение выражения:
1) 38 • х, если х = 10, 8, 5;
2) 409 + у, если у = 302, 501, 511;
3) а - 199, если а = 200, 800, 1000;
4) n : 7, если n = 140, 280, 980.
Ответ:
1) 38 • х
Если х = 10, то 38 • 10 = 380
Если х = 8, то 38 • 8 = 304
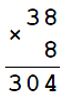
Если х = 5, то 38 • 5 = 190
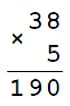
2) 409 + у
Если у = 302, то 409 + 302 = 711
Если у = 501, то 409 + 501 = 910
Если у = 511, то 409 + 511 = 920
3) а - 199
Если а = 200, то 200 - 199 = 1
Если а = 800, то 800 - 199 = 601
Если а = 1000, то 1000 - 199 = 799
4) n : 7
Если n = 140, то 140 : 7 = 20
Если n = 280, то 280 : 7 = 40
Если n = 980, то 980 : 7 = 140
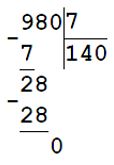
16. В бочке было 85 л воды. Сколько воды долили в бочку, если в ней стало 192 л?
Ответ:
192 - 85 = 107 л - воды долили в бочку
17. Ученик купил по одинаковой цене 9 тетрадей в линейку и 5 тетрадей в клетку. Каких тетрадей ученик купил больше и на сколько? За какие тетради он заплатил больше денег?
Ответ:
9 > 5 - значит, тетрадей в линейку ученик купил больше, чем в клетку
9 - 5 = 4 штуки - на столько больше ученик купил тетрадей в линейку, чем в клетку
Так как тетрадей в клетку ученик купил меньше, то за них он заплатил больше денег.
18. Ученик купил по одинаковой цене тетради в клетку и в линейку. Тетрадей в линейку он купил на 4 больше, чем в клетку, и поэтому заплатил за них на 12 р. больше. Какова цена тетради?
Ответ:
12 : 4 = 3 р. - цена тетради
Страница 9
19. Ученик купил по одинаковой цене 9 тетрадей в линейку и 5 тетрадей в клетку. За тетради в линейку он заплатил на 12 р. больше. Сколько стоили тетради в линейку? Сколько стоили тетради в клетку?
Ответ:
1) 9 - 5 = 4 штуки - на столько больше ученик купил тетрадей в линейку, чем в клетку
2) 12 : 4 = 3 р. - стоит одна тетрадь
3) 3 • 9 = 27 р. - стоят тетради в линейку
4) 3 • 5 = 15 р. - стоят тетради в клетку
20. Купили 4 м ткани за 320 р. Какова цена 1 м ткани? Какова стоимость 7 м этой ткани?
Ответ:
1) 320 : 4 = 80 р. - цена 1 м ткани
2) 80 • 7 = 560 р. - стоимость 7 м этой ткани
21. В трёх одинаковых ящиках 48 кг слив. Сколько слив в шести таких же ящиках?
Решите задачу двумя способами.
Ответ:
Способ 1.
1) 48 : 3 = 16 кг - слив в одном ящике
2) 16 • 6 = 96 кг - слив в шести ящиках
Способ 2.
1) 6 : 3 = 2 раза - во столько шесть ящиков больше, чем три ящика
2) 48 • 2 = 96 кг - слив в шести ящиках
22. Кепка стоит 126 р., перчатки на 67 р. дороже, чем кепка, а футболка стоит столько, сколько кепка и перчатки вместе. Какова цена футболки?
Ответ:
1) 126 + 67 = 193 р. - стоят перчатки
2) 126 + 193 = 319 р. - цена футболка
23. Для кабинета географии купили 5 глобусов по а р. и 7 карт по х р. Составьте выражение для вычисления стоимости покупки. Вычислите цену одного глобуса и одной карты, если стоимость всех купленных глобусов 900 р., а карт — 861 р.
Ответ:
Выражение для вычисления стоимости покупки: а • 5 + х • 7
1) 900 : 5 = 180 р. - цена одного глобуса
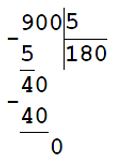
2) 861 : 7 = 123 р. - цена одной карты
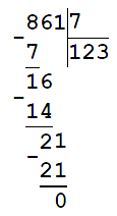
3) 180 • 5 + 123 • 7 = 900 + 861 = 1761 р. - стоимость покупки
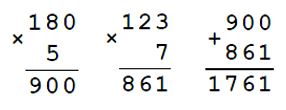
24. Ломаная линия длиной 90 см состоит из шести одинаковых по длине звеньев. Чему равна длина трёх звеньев этой ломаной?
Найдите решение задачи двумя способами.
Ответ:
1 способ.
1) 90 : 6 = 15 см - длина одного звена
2) 15 • 3 = 45 см - длина трех звеньев
2 способ.
1) 6 : 3 = 2 раза - во столько длина трех звеньев меньше, чем длина шести звеньев
2) 90 : 2 = 45 см - длина трех звеньев
Страница 10
25. Начертите окружность, длина радиуса которой 5 см. Отметьте точку А на этой окружности. Постройте квадрат АВХМ так, чтобы все его вершины лежали на этой окружности.
Ответ:
26. Площадь квадратной клумбы увеличили в 4 раза, сохранив её форму. Выскажите предположение о том, во сколько раз увеличили длину стороны этой клумбы.
Проверьте своё предположение, выполнив от руки рисунок.
Ответ:
27. Найдите и назовите пару отрезков, симметричных относительно оси ON.
Ответ:
Отрезок AB симметричен отрезку DС, так как он находится на таком же расстоянии от оси симметрии, что и отрезок DС.
28. Почему лучи АВ и CD не являются симметричными относительно оси ON?
Ответ:
Лучи АВ и CD не являются симметричными относительно оси ON, так как лучи направлены в разные стороны.
Т.е. начальная точка луча АС не симметрична начальной точке луча CD относительно оси ON.
29. Вырежьте из бумаги квадрат с длиной стороны 5 см. Разрежьте его по диагонали. Сложите из полученных частей треугольник.
Ответ:
Страница 11
30. Верно ли утверждение? Поясните свой ответ на примерах.
1) Число 250 делится не только на числа 2 и 5, но и на произведение этих чисел.
2) Число 24 делится не только на числа 8 и 2, но и на их произведение.
3) Если при пересечении диагоналей четырёхугольника образуются прямые углы, то этот четырёхугольник является квадратом.
4) Если в прямоугольнике провести прямую через середины противоположных сторон, то противоположные вершины прямоугольника будут симметричными относительно этой прямой.
Ответ:
1) Число 250 делится не только на числа 2 и 5, но и на произведение этих чисел. - верно
250 : 2 • 5 = 250 : 10 = 25
2) Число 24 делится не только на числа 8 и 2, но и на их произведение. - неверно
24 : 8 • 2 = 24 : 16 = 1 (ост. 8) - не делится без остатка
3) Если при пересечении диагоналей четырёхугольника образуются прямые углы, то этот четырёхугольник является квадратом. - верно
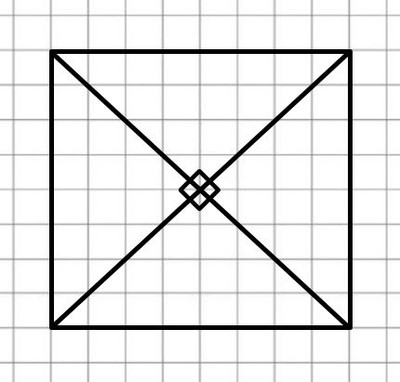
4) Если в прямоугольнике провести прямую через середины противоположных сторон, то противоположные вершины прямоугольника будут симметричными относительно этой прямой. - верно
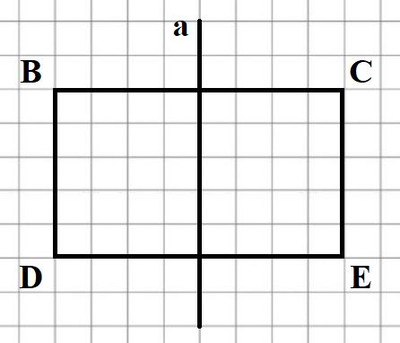
Если прямоугольник перегнуть по прямой a, то противоположные вершины прямоугольника совпадут, т.е. будут симметричными относительно этой прямой.
31. Вова решает задачу: «В прямоугольнике с длинами сторон 3 см и 4 см проведена диагональ длиной 5 см.
Вычислите периметр каждого из получившихся треугольников».
Для решения задачи Вова сделал рисунок.
Затем он составил план решения: «Прямоугольник разделился на два одинаковых треугольника.
Поэтому я сначала найду периметр прямоугольника, а затем разделю его на 2». В чём ошибка в рассуждении Вовы?
Ответ:
Страница 12
32. В таблице представлены данные об электротоварах, проданных в магазине в первом квартале года.
Ответьте на вопросы, используя данные таблицы.
Сколько утюгов продано в каждом месяце?
Сколько чайников продано в феврале; в марте?
В какие месяцы продано более 20 холодильников?
Верно ли, что наибольшее число холодильников продано в феврале?
Сколько чайников продано за три месяца?
Сколько указанных электротоваров продал магазин в марте?
Подсчитайте число проданных в январе утюгов и чайников.
На сколько больше продано в январе чайников, чем утюгов?
В каком месяце магазин продал наименьшее число чайников?
Ответ:
- Сколько утюгов продано в каждом месяце?
В январе - 54 утюга.
В феврале - 48 утюгов.
В марте - 60 утюгов.
- Сколько чайников продано в феврале; в марте?
В феврале - 65 чайников.
В марте - 28 чайников.
- В какие месяцы продано более 20 холодильников?
В феврале и марте.
- Верно ли, что наибольшее число холодильников продано в феврале?
Неверно, в феврале продано 22 холодильника, а в марте - 24.
24 > 22, значит, наибольшее число холодильников продано в марте.
- Сколько чайников продано за три месяца?
70 + 65 + 28 = 135 + 28 = 163 чайника
- Сколько указанных электротоваров продал магазин в марте?
60 + 28 + 24 = 88 + 24 = 112 электротоваров
- Подсчитайте число проданных в январе утюгов и чайников.
54 + 70 = 124 утюга и чайника
- На сколько больше продано в январе чайников, чем утюгов?
70 - 54 = 16 чайников
- В каком месяце магазин продал наименьшее число чайников?
В марте.
33. Имеется линейка длиной 20 см. Длина крышки стола больше длины линейки в 5 раз, а её ширина больше трёхкратной длины линейки на 13 см. Вычислите длину и ширину крышки стола.
Ответ:
1) 20 • 5 = 100 см - длина крышки стола
2) 20 • 3 = 60 см - трехкратная длина линейки
3) 60 + 13 = 73 см - ширина крышки стола
| Всего комментариев: 0 | |
