Страница 46
1. Рассмотри линии на рисунке.
Раздели эти линии на две группы: прямые и непрямые.
Назови номера прямых линий. Сколько их?
Назови номера непрямых линий. Сколько их?
Выскажи предположение, как по-другому можно назвать непрямые линии.
Можно ли назвать окружность кривой линией?
Ответ:
Прямые линии: 1, 3, 5 7. Их четыре.
Непрямые линии: 2, 4, 6. Их три.
Непрямые линии можно назвать кривыми линиями.
Окружность можно назвать кривой линией.
2. Прочитай название каждой прямой, называя буквы в разном порядке.
Ответ:
Первая прямая XY или YX.
Вторая прямая KM или MK.
Третья прямая AC или CA.
3. Начерти с помощью линейки пять различных прямых.
Ответ:
4. Начерти прямую, отметь на ней какую-нибудь точку. Сколько лучей образовалось?
Ответ:
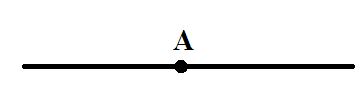
Образовалось два луча
Страница 47
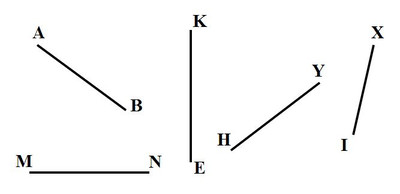
5. Какие из отмеченных точек лежат на прямой и какие на этой прямой не лежат?
Проверь свой ответ: используй линейку.
Ответ:
Прямая - это линия, которая не имеет начала и конца.
Точки, лежащие на прямой: Y, X, D, E, C.
Точки, не лежащие на прямой: K, A, M, B.
6. Вспомни и расскажи, как с помощью угольника построить прямой угол. Выскажи предположение о том, на каком рисунке при пересечении прямых образовались прямые углы.
Проверь своё предположение: используй угольник.
Ответ:
Построение прямого угла с помощью угольника:
1) Нужно отметить точку. Это вершина угла.
2) По линейке провести любой луч с началом в отмеченной точке. Это одна из сторон угла.
3) Приложить угольник так, чтобы вершина его прямого угла совпала с началом луча, а одна из его сторон совпала с направлением луча.
4) Провести луч с началом в отмеченной точке по направлению второй стороны прямого угла угольника. Это вторая сторона угольника.
Построение закончено.
На первом рисунке при пересечении прямых образовались прямые углы.
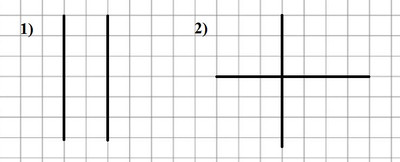
7. Начерти две прямые, которые при пересечении образуют прямой угол: 1) на листе в клетку; 2) на альбомном листе.
Для каждого случая составь план выполнения чертежа: с чего начнёшь, что будешь делать потом. Какими инструментами воспользуешься в каждом случае?
Ответ:
Страница 48
8. На каких рисунках прямые пересекаются и на каких не пересекаются? Есть ли на рисунке прямые, пересекающиеся под прямым углом?
Проверь свои ответы: используй линейку и угольник.
Ответ:
Прямые пересекаются на рисунках: а, б, г.
Прямые не пересекаются на рисунке в.
Прямые, пересекающееся под прямым углом - на рисунке г.
9. Определи на глаз, какая из тропинок самая короткая. Проверь свой ответ измерением.
Какой угол составляют дорога и самая короткая тропинка?
Ответ:
Страница 49
10. Какая из отмеченных точек ближе всех остальных к прямой ХО? Поясни свой ответ.
Ответ:
Ближе всего к прямой ХО находится точка М, так как она находится на расстоянии одной клетки от прямой. Точка Б находится на расстоянии 1,5 клетки, а точка А - 2 клетки.
11. Рассмотри рисунок. Пересекаются ли железнодорожные рельсы; электрические провода?
Ответ:
Железнодорожные рельсы не пересекаются.
Электрические провода не пересекаются.
12. Как тебе кажется, какие прямые не пересекаются?
Ответ:
Голубые прямые не пересекаются.
13. Начерти в тетради две прямые, которые:
1) не пересекаются;
2) пересекаются, образуя прямой угол.
Ответ:
Страница 50
14. Назови результаты умножения.
40 • 8 7 • 20 200 • 3 4 • 100
60 • 6 9 • 50 300 • 2 80 • 10
Выпиши пары выражений, которые имеют равные значения.
Ответ:
40 • 8 = 320 7 • 20 = 140 200 • 3 = 600 4 • 100 = 400
60 • 6 = 360 9 • 50 = 450 300 • 2 = 600 80 • 10 = 800
Пары выражений, которые имеют равные значения:
200 • 3 = 600
300 • 2 = 600
15. Найди устно значения выражений и запиши ответы в три столбца:
в первый — однозначные числа, во второй — двузначные, а в третий столбец — трёхзначные.
60 - 8 • 5 (81 - 9) : 9 + 18 : 9
49 : 7 - 7 (54 : 6 - 9) • 7 + 162
Ответ:
60 - 8 • 5 = 60 - 40 = 20
49 : 7 - 7 = 7 - 7 = 0
(81 - 9) : 9 + 18 : 9 = 72 : 9 + 18 : 9 = 8 + 2 = 10
(54 : 6 - 9) • 7 + 162 = (9 - 9) • 7 + 162 = 0 • 7 + 162 = 0 + 162 = 162
Однозначные Двузначные Трехзначные
числа числа числа
0 10; 20 162
16. Длина прямоугольного участка земли 8 м, а ширина — в 2 раза меньше длины. Какова площадь участка? Какова длина границы этого участка?
Ответ:
1) 8 : 2 = 4 м - ширина участка
2) 8 • 4 = 32 м2 - площадь участка
3) (8 + 4) • 2 = 12 • 2 = 24 м - длина границы участка, т.е. периметр участка
17. Площадь прямоугольника равна 56 дм2, его длина — 7 дм. Вычисли периметр этого прямоугольника.
Ответ:
1) 56 : 7 = 8 дм - сторона прямоугольника
2) (7 + 8) • 2 = 15 • 2 = 30 дм - периметр прямоугольника
18. В магазин привезли 4 коробки с кастрюлями, по 6 кастрюль в каждой, и сковородки. Сковородок в 3 раза меньше, чем кастрюль. Сколько посуды привезли в магазин?
Ответ:
1) 4 • 6 = 24 кастрюли - привезли всего
2) 24 : 3 = 8 сковородок - привезли всего
3) 24 + 8 = 32 штуки - посуды привезли в магазин
19. Составь задачу и выбери выражение, которым можно записать её решение.
Ответ:
Маша купила линейку за 9 р. и три одинаковые ручки за 18 р. Сколько бы денег заплатила Маша, если бы она купила линейку и одну ручку?
9 + 18 : 3 = 9 + 6 = 15 р. - заплатила бы Маша за линейку и одну ручку
Страница 51
20. Два двадцатилитровых бидона полностью наполнены молоком. Из первого бидона сначала вылили четверть всего молока, а потом — пятую часть оставшегося молока. Из второго бидона сначала вылили пятую часть молока, а потом ещё четверть оставшегося молока. Выскажи предположение о том, разное или одинаковое количество молока стало в бидонах.
Проверь своё предположение: выполни вычисления.
Ответ:
Одинаковое количество молока стало в бидонах, так как изначально количество молока в двух бидонах было одинаковым, и вылили из двух бидонов одно и то же количество молока.
1) 20 : 4 = 5 литров - молока вылили из первого бидона
2) 20 - 5 = 15 литров - молока осталось в первом бидоне
3) 15 : 5 = 3 литра - молока вылили еще раз из первого бидона
4) 15 - 3 = 12 литров - молока стало в первом бидоне
5) 20 : 5 = 4 литра - молока вылили из второго бидона
6) 20 - 4 = 16 литров - молока осталось во втором бидоне
7) 16 : 4 = 4 литра - молока вылили еще раз из второго бидона
8) 16 - 4 = 12 литров молока стало во втором бидоне
Таким образом, одинаковое количество молока стало в бидонах.
21. На тарелке лежат вишни. Петя взял половину всех вишен, Катя — половину оставшихся вишен, а Нине достались последние 4 вишни. Сколько вишен было на тарелке?
Ответ:
22. Прочитай слово.
Сколько осей симметрии имеет фигура на рисунке?
Ответ:
Слово - ключи.
Фигура имеет 5 осей симметрии.
Страница 52
23. Из двух листов картона сделали 8 папок. Сколько папок получится из 9 таких листов картона?
Ответ:
1) 8 : 2 = 4 папки - можно сделать из одного листа картона
2) 9 • 4 = 36 папок - получится из 9 листов картона
24. Какое число должно быть написано в окошке, чтобы равенство было верным?
1) □ • 8 = 56 2) □ : 6 = 7
Ответ:
1) 56 : 8 = 7
Проверка: 7 • 8 = 56
2) 7 • 6 = 42
Проверка: 42 : 6 = 7
25. Вычисли значение буквенного выражения 264 + х, если х = 36, 250, 736.
Ответ:
264 + х
Если х = 36, то 264 + 36 = 300
Если х = 250, то 264 + 250 = 515
Если х = 736, то 264 + 736 = 1000
26. Вычисли значение выражения 6 • а, если а = 0, 1, 5, 7, 10.
Ответ:
6 • а
Если а = 0, то 6 • 0 = 0
Если а = 1, то 6 • 1 = 6
Если а = 5, то 6 • 5 = 30
Если а = 6, то 6 • 6 = 36
Если а = 10, то 6 • 10 = 60
27. Найди значение выражения с : 3, если с = 12, 27, 18.
Ответ:
с : 3
Если с = 12, то 12 : 3 = 4
Если с = 27, то 27 : 3 = 9
Если с = 18, то 18 : 3 = 6
28. Посадили 7 дубов и k клёнов. Сколько деревьев посадили?
Подставь вместо буквы k числа 5, 8, 9. Прочитай получившиеся задачи и реши их. Составь выражение для решения задачи с буквой k.
Ответ:
Выражение для решения задачи с буквой k.
7 + k
1) При k = 5
Посадили 7 дубов и 5 клёнов. Сколько деревьев посадили?
7 + 5 = 12 деревьев
2) При k = 8
Посадили 7 дубов и 8 клёнов. Сколько деревьев посадили?
7 + 8 = 15 деревьев
3) При k = 9
Посадили 7 дубов и 9 клёнов. Сколько деревьев посадили?
7 + 9 = 16 деревьев
29. Назови треть каждого из чисел: 21, 18, 27, 12, 30.
Назови число, если его четвёртая часть равна: 8, 9, 7, 3, 1.
Ответ:
21 : 3 = 7 - треть числа 21
18 : 3 = 6 - треть числа 18
27 : 3 = 9 - треть числа 27
12 : 3 = 4 - треть числа 12
30 : 3 = 10 - треть числа 30
8 • 4 = 32
9 • 4 = 36
7 • 4 = 28
3 • 4 = 12
1 • 4 = 4
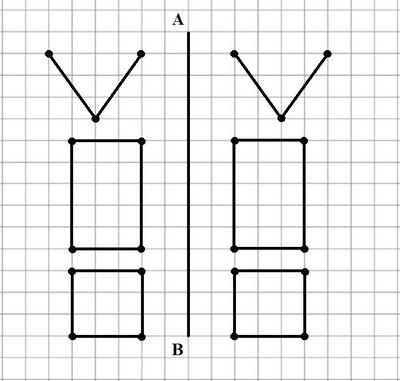
30. Скопируй чертёж в тетрадь и изобрази фигуры, симметричные данным относительно оси АВ.
Ответ:
31. По какому правилу составлена цепочка чисел?
Назови три следующих числа цепочки.
Составь свою цепочку из четырёх чисел так, чтобы первое число было равно 125, а каждое следующее на 25 больше предыдущего.
Ответ:
Каждое следующее число на 150 меньше предыдущего.
три следующих числа цепочки: 300, 150, 0.
125 150 175 200
Страница 54
32. Юре а лет. Катя на 3 года моложе Юры. Сколько лет Кате?
Подставь вместо буквы а числа 9, 10, 11. Прочитай получившиеся задачи и реши их. Составь выражение для решения задачи с буквой а.
Ответ:
Выражение для решения задачи с буквой а.
а - 3
1) При а = 9
Юре 9 лет. Катя на 3 года моложе Юры. Сколько лет Кате?
9 - 3 = 6 лет
1) При а = 10
Юре 10 лет. Катя на 3 года моложе Юры. Сколько лет Кате?
10 - 3 = 7 лет
1) При а = 11
Юре 11 лет. Катя на 3 года моложе Юры. Сколько лет Кате?
11 - 3 = 8 лет
33. Груши и яблоки разложили в пакеты, по 2 груши и 3 яблока в каждом. Сколько потребовалось пакетов, если всего было разложено 40 фруктов?
Ответ:
1) 2 + 3 = 5 фруктов - в одном пакете
2) 40 : 5 = 8 пакетов - потребовалось
34. Каждому из восьмерых детей купили 5 воздушных шаров. Трое из них попросили купить им ещё по 2 шара. Сколько всего шаров получили дети? Реши задачу двумя способами.
Ответ:
1 способ.
1) 8 • 5 = 40 шаров - купили всем детям
2) 3 • 2 = 6 шаров - еще купили трем детям
3) 40 + 6 = 46 шаров - всего получили дети
2 способ.
1) 5 + 2 = 7 шаров - по столько получил каждый из трех детей
2) 3 • 7 = 21 шар - получили трое детей
3) 8 - 3 = 5 детей - получили по 5 воздушных шаров
4) 5 • 5 = 25 шаров - получили пять детей
5) 21 + 25 = 46 шаров - всего получили дети
35. Любой квадрат является прямоугольником.
У квадрата 4 оси симметрии. Значит, у любого прямоугольника тоже 4 оси симметрии.
Верен ли ход рассуждений и вывод? Поясни свой ответ.
Ответ:
36. Подсчитай, чему равна: половина суммы чисел 11 и 7; треть разности чисел 86 и 59; четвёртая часть произведения чисел 3 и 8; пятая часть частного 30 и 6.
Ответ:
(11 + 7) : 2 = 18 : 2 = 9 - половина суммы чисел 11 и 7
(86 - 59) : 3 = 27 : 3 = 9 - треть разности чисел 86 и 59
3 • 8 : 4 = 24 : 4 = 6 - четвёртая часть произведения чисел 3 и 8
30 : 6 : 5 = 5 : 5 = 1 - пятая часть частного 30 и 6
37. Найди закономерность в расположении значений длины:
8 мм, 1 см 3 мм, 1 см 8 мм, 2 см 3 мм.
Назови следующие три значения.
Ответ:
Каждое последующее значение длины на 5 мм больше предыдущего.
8 мм, 1 см 3 мм, 1 см 8 мм, 2 см 3 мм, 2 см 8 мм, 3 см 3 мм, 3 см 8 мм.
| Всего комментариев: 0 | |
